GEM hypothesis is a conceptual framework to analyze movement variability in redundant systems. It was initially developed by Cusumano [1] in 2006 to study the relationship between variability at the body and goal levels using sensitivity analysis.
This approach like, the other geometry-based approaches such as uncontrolled manifold hypothesis (UCM) [2] and minimal intervention principle (MIP), addresses the issue of equifinality in motor tasks. All these approaches share the idea that the excess of body-level degree of freedom over those at the task-goal level gives rise to an entire set of motor solutions, assumed to have the structure of a manifold in the space of body-level state variables. This is simply the mathematical consequence of the fact that the space of body-state variables needed to perform a task has significantly greater dimensionality than the space that is needed to define the task. Any point in this manifold represents a goal-equivalent solution to a given task that is achieved by a combination of body-level state variables. In other words, all solutions in this manifold result in successful achievement of the task. In this approach, task manifold is defined by concept of goal function that mathematically encodes interactions between body variables, goal variables and the environment needed for perfect task execution.
This conception can be realized by partitioning the variability in the space of body variables in to a component that is tangential to the manifold and a component that is orthogonal to it. The component tangential to the manifold is goal equivalent as variability in this space caused no variability at the level of task variables. Alternatively, the component orthogonal to the manifold is consistent with variability at the task level and results in performance error so; it is more controlled by the controller.
For example consider Fig. A, if the primary goal of a task is to be matched with metronome frequency or to maintain the movement time (T) with metronome on each movement cycle, all combinations of movement distance (D) and movement speed (S) that satisfy this goal define the GEM for this task as long as D/S = T. Given the existence of this GEM, variability in the space of body parameters (D and S), can be decomposed in to components that directly affect achieving the task goal and those that have no effect on the performance. So, variability in S (i), D (i) are decomposed in to variability tangent ( δT) to and perpendicular (δP), to the GEM.
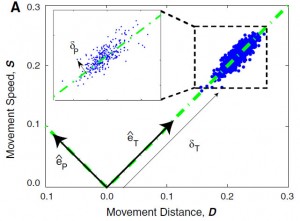Figure A: an example of GEM analysis [3]. The green line is the GEM. Each blue point is supposed to be on the GEM, but the variability of the subject in choosing S and D, results in a point cloud, which can be decomposed tangent and perpendicular to GEM.
GEM approach has many features that distinguish it from other approaches to movement fluctuation analysis that are based on goal equivalence. First, it emphasizes that the task manifold or goal equivalence is a basic property of redundant systems and exists independent of any specific control scheme. Meaning, this is not designed to search for actual control variables by making a priori assumption about the aspects of performance, which is controlled. Thus, GEM can be defined even for completely uncontrolled or open loop systems. Second, this approach distinguishes between passive and active contribution to goal-level variability by accounting sensitivity properties along the GEM and also stability of fluctuation dynamics near the GEM. So, the GEM approach bridges the gap between geometry-based approaches which focus on the role of motor redundancy and dynamical methods which deal with the regulation of variability during repeated performances.
Briefly, this approach focuses on precisely characterizing how task performance is related to body variability observed during repeated performance of a task without attempting to identify the nature of the control used to regulate them. This approach also addresses the issue of sensitivity of performance to body errors that together with purely geometrical factors gives a complete picture of variability generation at the goal. Study of both task sensitivity and geometry without analytical model and from experimental data is possible by this method.
References:
1. Cusumano, J.P. and P. Cesari, Body-goal variability mapping in an aiming task. Biological Cybernetics, 2006. 94(5): p. 367-379.
2. Scholz, J.P. and G. Schöner, The uncontrolled manifold concept: identifying control variables for a functional task. Experimental Brain Research, 1999. 126(3): p. 289-306.
3. Gates, D.H. and J.B. Dingwell, The effect of neuromuscular fatigue on task performance during repetitive goal-directed movements. Experimental Brain Research, 2008. 187(4): p. 573-585.